Points of concurrency of a triangle – Points of concurrency, the enigmatic intersections of lines within a triangle, unveil a captivating chapter in triangle geometry. These special points, each possessing unique properties and relationships, serve as a cornerstone for solving countless triangle problems and find applications across diverse fields.
As we delve into the intricacies of centroids, incenters, circumcenters, and orthocenters, we uncover a tapestry of geometric elegance and algebraic precision. Their properties, interconnectedness, and historical evolution paint a rich narrative that illuminates the profound significance of points of concurrency in the realm of mathematics.
Introduction
The points of concurrency of a triangle are the points where the three internal angle bisectors, three medians, and three perpendicular bisectors of the sides of the triangle intersect.
These points are significant because they provide valuable information about the triangle’s properties, such as its centroid, orthocenter, and incenter.
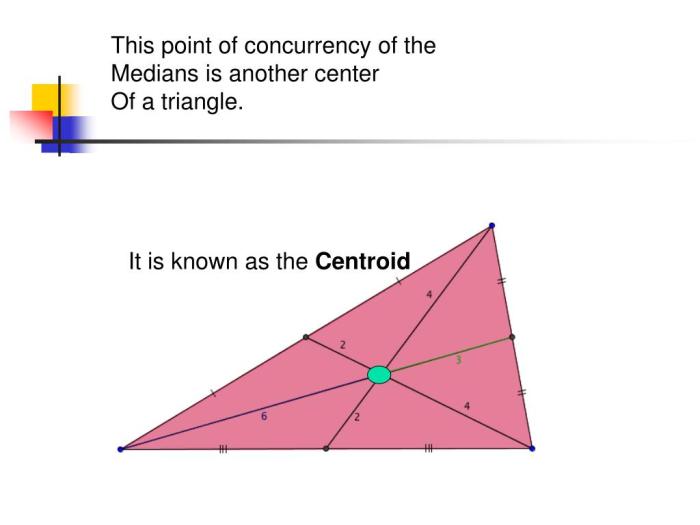
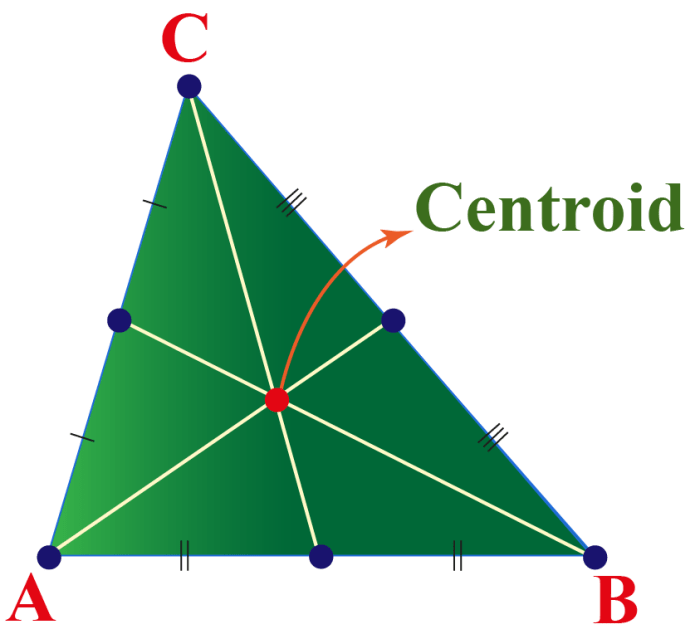
Centroid
The centroid is the point of intersection of the three medians of a triangle. It is the center of gravity of the triangle and divides each median in a ratio of 2:1.
Orthocenter
The orthocenter is the point of intersection of the three altitudes of a triangle. It is the point where the three perpendicular bisectors of the sides of the triangle meet.
Incenter
The incenter is the point of intersection of the three internal angle bisectors of a triangle. It is the center of the inscribed circle of the triangle, which is the largest circle that can be inscribed in the triangle.
Types of Points of Concurrency
In geometry, a point of concurrency is a point where two or more lines, segments, or other geometric objects intersect. In the case of a triangle, there are four notable points of concurrency:
Centroid
The centroid is the point of intersection of the three medians of a triangle. A median is a line segment that connects a vertex to the midpoint of the opposite side. The centroid is also known as the center of gravity or the barycenter of the triangle.
It is the point at which a triangle would balance if it were suspended from this point.
The coordinates of the centroid of a triangle with vertices (x1, y1), (x2, y2), and (x3, y3) are:
(xc, y c) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
Incenter
The incenter is the point of intersection of the three angle bisectors of a triangle. An angle bisector is a line segment that divides an angle into two equal angles. The incenter is the center of the inscribed circle of the triangle, which is the largest circle that can be drawn inside the triangle and tangent to all three sides.
The coordinates of the incenter of a triangle with vertices (x1, y1), (x2, y2), and (x3, y3) are:
(xi, y i) = ((ax1 + bx2 + cx3)/(a + b + c), (ay1 + by2 + cy3)/(a + b + c))
where a = √(x2 – x3)² + (y2 – y3)², b = √(x3 – x1)² + (y3 – y1)², and c = √(x1 – x2)² + (y1 – y2)².
Properties of Points of Concurrency: Points Of Concurrency Of A Triangle
Points of concurrency exhibit distinct properties and relationships that define their significance in triangle geometry. These properties provide valuable insights into the behavior and characteristics of triangles and their constituent points.
One fundamental property is the harmonic conjugate relationship. For any two distinct points of concurrency, P and Q, on a triangle, there exists a third point, R, such that P, Q, and R are collinear and the cross-ratio of (P, Q; A, R) is -1. This property implies that the harmonic conjugate of a point of concurrency with respect to two other points of concurrency lies on the same line.
Another important property is the Cevian triangle relationship. For any three points of concurrency, A, B, and C, on a triangle, the Cevian triangle formed by the lines connecting these points to the opposite vertices is similar to the original triangle. This property provides a geometric connection between the points of concurrency and the triangle itself.
Incenter and Excenters, Points of concurrency of a triangle
- The incenter, the center of the inscribed circle, is equidistant from the three sides of the triangle.
- The circumcenter, the center of the circumscribed circle, is equidistant from the three vertices of the triangle.
- The orthocenter, the intersection of the three altitudes, is the point where the perpendiculars from the vertices to the opposite sides intersect.
Centroid and Medians
- The centroid, the point of intersection of the three medians, divides each median in a ratio of 2:1.
- The medians, the lines connecting the vertices to the midpoints of the opposite sides, are concurrent at the centroid.
- The centroid divides the area of the triangle into three equal parts.
Applications of Points of Concurrency
Points of concurrency play a vital role in solving triangle problems and have practical applications in various fields.
In navigation, the centroid is used to determine the center of gravity of a ship, which is crucial for maintaining stability and balance. The orthocenter is used to find the line of action of the gravitational force acting on the ship.
Surveying
In surveying, the circumcenter is used to establish the center of a circle that passes through three non-collinear points. This circle is used as a reference for determining the positions of other points in the area being surveyed.
Engineering
In engineering, the incenter is used to determine the minimum radius of a circle that can be inscribed within a triangle. This information is useful in designing structures that require precise measurements and tolerances.
5. Historical Development
The concept of points of concurrency in triangles has a long and rich history, with contributions from mathematicians throughout the ages.
The earliest known work on points of concurrency can be traced back to the ancient Greeks, who studied the properties of triangles and other geometric figures. In particular, the Greek mathematician Euclid, who lived in the 3rd century BC, is credited with discovering the properties of the centroid, the point where the medians of a triangle intersect.
Archimedes
Another notable Greek mathematician who made significant contributions to the study of points of concurrency was Archimedes, who lived in the 2nd century BC. Archimedes discovered the properties of the orthocenter, the point where the altitudes of a triangle intersect.
Apollonius
In the 3rd century AD, the Greek mathematician Apollonius of Perga made further contributions to the study of points of concurrency. Apollonius discovered the properties of the circumcenter, the point where the perpendicular bisectors of the sides of a triangle intersect.
Later Developments
In the centuries that followed, mathematicians continued to study points of concurrency and their properties. In the 17th century, the French mathematician René Descartes developed analytic geometry, which allowed for a more rigorous and systematic study of geometric figures. Descartes used analytic geometry to derive the equations of the lines that connect the vertices of a triangle to its points of concurrency.
In the 19th century, the German mathematician Karl Wilhelm Feuerbach made significant contributions to the study of points of concurrency. Feuerbach discovered the nine-point circle, a circle that passes through nine special points associated with a triangle, including the centroid, the orthocenter, and the circumcenter.
Modern Developments
In the 20th century, the study of points of concurrency continued to flourish. Mathematicians developed new techniques and results, and the subject became an important area of research in geometry.
FAQ Insights
What is the significance of points of concurrency in triangle geometry?
Points of concurrency provide crucial reference points within a triangle, allowing for the precise measurement of angles, distances, and areas.
How are points of concurrency used in solving triangle problems?
Points of concurrency serve as anchors for constructing lines, circles, and other geometric figures that aid in solving a wide range of triangle-related problems.